Robust Bounding Box Fusion with Combinatorial Optimization

This is part 1/2 of a series on postprocessing tricks I used to generate a large custom synthetic dataset on a shoestring budget. Read the second part

The Concrete Problem

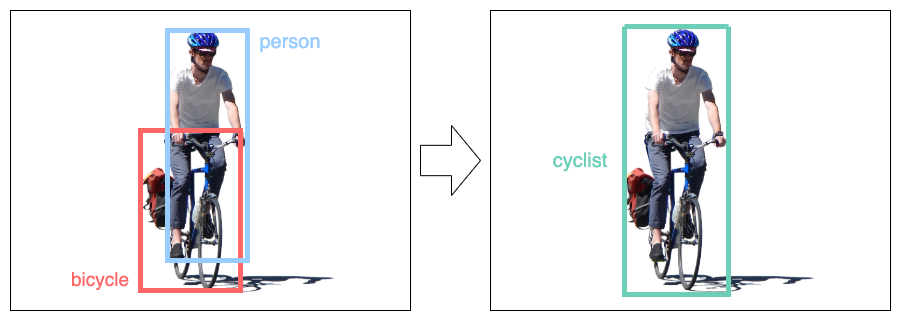
I am trying to build an object detection model that can identify cyclists. Public datasets like COCO contain ‘person’ and ‘bicycle’ categories, but no ‘cyclist’ category. It would be great if I could use pre-trained models to either merge bounding boxes at inference time, or merge them to create a synthetic dataset that has a ‘cyclist’ category. Either way, the question is:

Is there an algorithm that can correctly and efficiently pair associated bounding boxes?

The “Too Simple” Solution

This sounds easy: Find all instances of ‘person’ boxes overlapping with ‘bicycles’ boxes, and replace them with a ‘cyclist’ box!

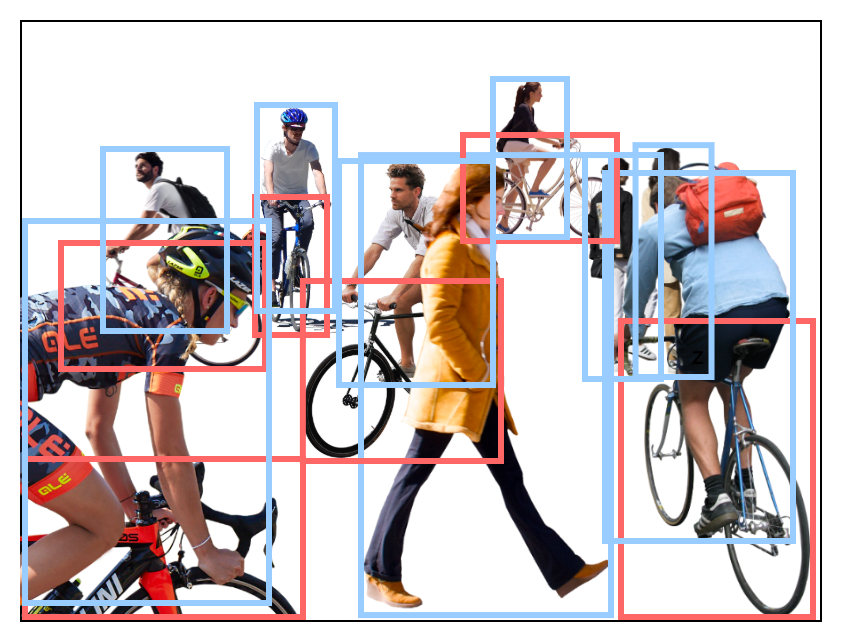
Unfortunately, this will fail if there are crowds or multiple overlaps, because this algorithm has no criteria for choosing the best pairing among many. Furthermore, the order in which we find and replace bounding boxes becomes critical yet finding some optimal order becomes exponentially costly for larger sets.

Instead of coming up with ad-hoc fixes to this that issue, let’s abstract this problem a bit.

Abstracting the Problem

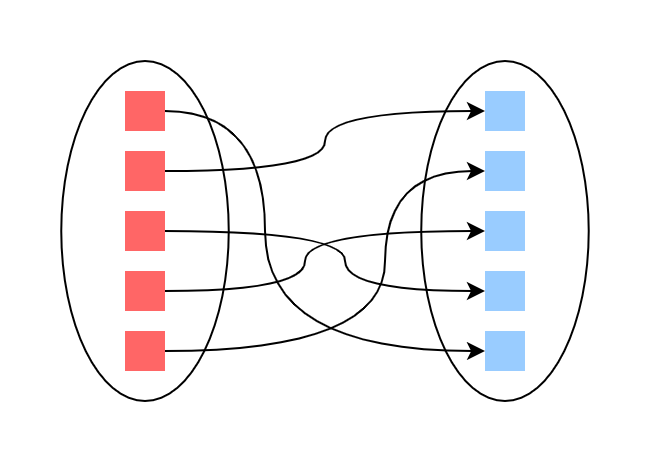
The insight here is that this is an assignment problem, where a ‘bicycle’ bounding box needs to be paired up with a ‘person’ bounding box, in such a way that maximizes the total intersection-over-union (IOU) ( i.e. bounding box overlap) of all pairings.

In our assignment problem, the cost matrix can be defined by the IOU between two boxes. Even better news for us: some very smart people have figured out how to calculate it in polynomial time.

More about the assignment problem / Hungarian algorithm:

• https://brilliant.org/wiki/hungarian-matching/
• http://www.assignmentproblems.com/doc/LSAPIntroduction.pdf

The Practical Solution

We’ll use this example to step through the whole process:

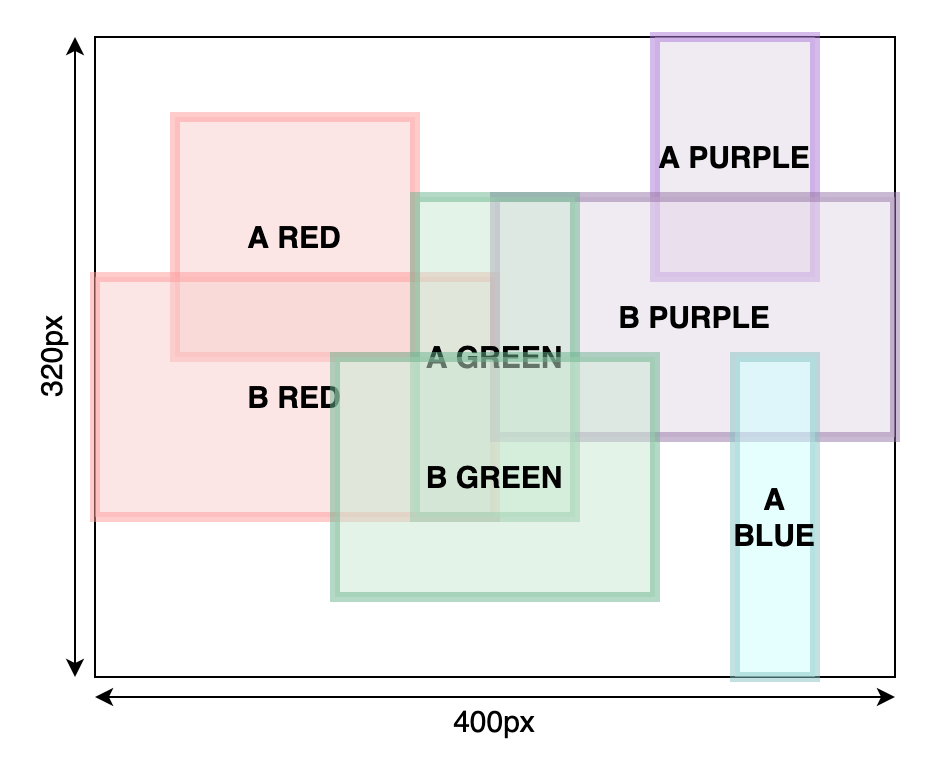
‘A’ and ‘B’ are category names, and colors represent the correct (desired) pairing.

a_red = [40, 40, 160, 160]
b_red = [0, 120, 200, 240]
a_green = [160, 80, 240, 240]
b_green = [120, 160, 280, 280]
a_purple = [280, 0, 360, 120]
b_purple = [200, 80, 400, 200]
a_blue = [320, 160, 360, 320]

We will be importing numpy and scipy today.

>>> import numpy as np
>>> import scipy.optimize

First, we calculate the IOU for all pairs in category (A,B).

>>> def iou(boxes1, boxes2):
        '''
        Vectorized intersection-over-union
        '''
        x11,y11,x12,y12 = np.split(boxes1, 4, axis=1)
        x21,y21,x22,y22 = np.split(boxes2, 4, axis=1)
        
        xA = np.maximum(x11, np.transpose(x21))
        yA = np.maximum(y11, np.transpose(y21))
        xB = np.minimum(x12, np.transpose(x22))
        yB = np.minimum(y12, np.transpose(y22))
        
        interArea = np.maximum((xB - xA + 1), 0 ) * np.maximum((yB-yA + 1), 0)

        boxAArea = (x12-x11+1) * (y12-y11+1)
        boxBArea = (x22-x21+1) * (y22-y21+1)
        
        iou = interArea / (boxAArea + np.transpose(boxBArea) - interArea)
        
        return iou

>>> As = np.array([a_red, a_green, a_purple, a_blue])
>>> Bs = np.array([b_red, b_green, b_purple])

>>> iou_matrix = iou(As, Bs)
>>> iou_matrix
np.array([0.15, 0.  , 0.  ],
         [0.15, 0.25, 0.15],
         [0.  , 0.  , 0.11],
         [0.  , 0.  , 0.06]])

Halfway there! We now have an adjacency matrix with IOU values representing ‘cost’.

There are several packages that implement linear sum assignment problem solvers.

I used scipy.optimize.linear_sum_assignment. See lapsolver README for a speed comparison.

In most demonstrations, the goal is to minimize the cost. In our case, however, we want to maximize the total IOU.

>>> assignment = scipy.optimize.linear_sum_assignment(iou_matrix, maximize=True)
>>> assignment
(array([0,1,2]), array([0,1,2]))

Awesome! This tells us that the correct assignment is:

(0,0) -> (a_red, b_red)
(1,1) -> (a_green, b_green)
(2,2) -> (a_purple, b_purple)

note that we don’t see (3,_), which would refer to a_blue, which makes sense because it is not paired with any other box.

Now, all that is left to do is calculate the new bounding box coordinates from its source pair, and delete the old bounding boxes. I have left out that part because it is trivial.

Epilogue

I hope this post showed you how combinatorial optimization, and the assignment problem in particular, can be helpful in elegantly solving problems. This is just one of the many uses for linear assignment problem solvers within the velovision codebase.